A Teoria da Resposta ao Item, muitas vezes abreviada apenas por TRI, é uma modelagem estatística utilizada em medidas psicométricas, principalmente na área de avaliação de habilidades e conhecimentos.
Índice |
Aplicação
A aplicação mais freqüente da Teoria da Resposta ao Item são as avaliações de habilidades e conhecimentos em Testes de Múltipla escolha. A Teoria da Resposta ao Item, contudo, pode abranger também testes dissertativos além de poder abarcar várias outras áreas onde se deseja obter uma medida indireta de alguma característica, por exemplo: estimar a altura de uma pessoa através de um questionário com perguntas indiretas como "Você costuma abaixar a cabeça ao passar por uma porta?" onde sabemos que as respostas "sim" e "não" estão correlacionadas com a característica a ser medida indiretamente, no caso a altura da pessoa. Outras áreas proeminentes para a aplicação da Teoria da Resposta ao Item são os Testes Psicológicos e questionários em geral, com destaque para questionários que meçam o nível sócio-econômico dos pesquisados.
A Teoria da Resposta ao Item é utilizada em avaliações de vários países, onde os programas de avaliação mais conhecidos são o NAEP[1] nos Estados Unidos da América, o ETS[2] nos Estados Unidos da América, o GMAT[3] nos Estados Unidos da América, o CITO[4] na Holanda e vários outros. No Brasil o principal programa de avaliação que utiliza a Teoria da Resposta ao Item é o SAEB, que desde sua criação em 1995 a utiliza para estimar as habilidades e conhecimentos dos alunos do Ensino Básico e Médio das escolas públicas brasileiras através de amostragem do universo desses alunos. A partir de 2005 esta avaliação busca avaliar de forma censitária toda a rede pública do país. O novo Enem, reformulado a partir de 2009, também faz uso da TRI, de forma a garantir a comparabilidade das notas entre diferentes edições. Esta foi a aplicação de maior impacto na divulgação da Teoria da Resposta ao Item.
História
A Teoria da Resposta ao Item surgiu a partir de discussões teóricas sobre a viabilidade de se comparar as habilidades e os conhecimentos de examinandos submetidos a provas diferentes. A Teoria Clássica dos Testes, principal teoria estatística para medida dessas características na época, via-se diante de enormes dificuldades para comparar as habilidades e os conhecimentos de examinandos submetidos a provas diferentes. Nesse sentido, em 1950, Gulliksen, H definiu, no âmbito da Teoria Clássica dos Testes que duas provas podem ser consideradas formas paralelas quando, após a conversão para a mesma escala, suas médias, desvios padrão de acertos bem como demais correlações do número de acertos com todo e qualquer outro critério fossem iguais. Em 1971, ainda no âmbito da Teoria Clássica dos Testes, Angoff, W delimita a equivalência de provas ao apresentar as seguintes exigências:
- As provas devem medir a mesma característica ou habilidade;
- A equivalência estabelecida deve ser independente dos dados em particular utilizados para estabelecer esse princípio e deve ser aplicável em todas as situações parecidas;
- Os escores de duas provas, uma vez estabelecida sua equivalência, devem ser substituíveis entre si, e;
- A equivalência deve ser simétrica, ou seja, não deve fazer distinção entre a prova particular escolhida como base de referência.
Ainda no âmbito da Teoria Clássica dos Testes, em 1977, Lord, F M estende as considerações levantadas por Angoff. A noção de escores substituíveis ganha nova dimensão com a introdução do conceito de equidade: Os escores transformados y* e observados x podem ser considerados "equivalentes" quando houver indiferença se um examinando responder a prova X ou Y. De acordo com esse princípio:
- Torna-se inviável a tentativa de se estabelecer a equivalência entre provas que medem diferentes características ou habilidades (consistente com a primeira restrição de Angoff);
- A equivalência de escores com margens de erro desiguais não pode ser estabelecida (consistente com os escores substituíveis de Angoff);
- Não se pode estabelecer a equivalência de provas que refletem diferentes níveis de dificuldades.
Segundo Lord, se as provas X e Y têm dificuldades diferentes, a relação entre seus escores verdadeiros é necessariamente não linear devido aos efeitos de piso e de teto. Se duas provas têm uma relação não linear é implausível que elas sejam igualmente fidedignas em todos os grupos de examinandos. Isso leva à conclusão incômoda de que, a rigor, não se pode tornar equivalentes os escores observados em provas de dificuldades diferentes. Todo esse panorama levou Lord a defender as vantagens teóricas dos modelos da teoria da resposta ao item em procedimentos que estabelecem a equivalência dos resultados de provas.
Fundamentos
A Teoria da Resposta ao Item trata o problema da estimação da habilidade e conhecimento de um examinando de forma essencialmente diferente: o enfoque das análises desvincula-se das provas (Teoria Clássica dos Testes) e concentra-se nos Itens; se na Teoria Clássica dos Testes as estatísticas dos itens dependem da população dos examinandos e da prova à qual os itens pertencem, na Teoria da Resposta ao Item cria-se o conceito de que os parâmetros dos itens, obtidos no processo estatístico de "calibração" dos parâmetros de dificuldade, discriminação e acerto casual dos itens (Valle, R) são características próprias dos mesmos. Costuma-se considerar que a característica de medição dos Itens, representados por seus parâmetros, são invariantes no tempo com algumas ressalvas, por exemplo: um item que aborde o conhecimento sobre eclipses solares e lunares estará sujeito a variações de suas características de medição conforme o modismo, sobretudo quando um eclipse ocorre; em casos como esse, a invariância dos parâmetros do item no tempo não deve ser considerada como verdadeira. Consideradas as ponderações anteriores, uma característica fundamental para a viabilidade de comparação da habilidade e conhecimento de examinandos submetidos a provas diferentes é que a Teoria da Resposta ao Item modela a probabilidade de acerto a um item, também conhecida como Curva Característica do Item, através de uma função não linear do conhecimento dos examinandos. Essa característica da modelagem da Teoria da Resposta ao Item é de grande importância pois, desse modo, é possível comparar o conhecimento dos examinandos submetidos a provas diferentes sendo necessário apenas que as provas meçam as mesmas características; essa propriedade é essencialmente útil para sistemas de avaliações onde é possível submeter uma grande quantidade de tópicos de uma matéria em sala de aula (útil para se ter um painel geral sobre o ensino de vários tópicos) com os alunos respondendo apenas um conjunto pequeno dos itens utilizados na avaliação (útil para não tornar as provas excessivamente extensas). Uma boa referência sobre o assunto é Andrade, D.F, Tavares, H.R. & Valle, R.C. (2000).
Modelagem Estatística
A modelagem mais moderna para a Teoria da Resposta ao Item utiliza a Estatística Bayesiana. Nessa modelagem, a probabilidade de acerto de um item é condicionada à habilidade e conhecimento do examinando. A curva que modela a probabilidade de acerto de um item é uma função crescente na ordenada da habilidade e conhecimento; o gráfico que tem a probabilidade condicional de acerto de um item na ordenada e a habilidade e conhecimento na abscissa é conhecido como Curva Característica do Item.
Na abordagem bayesiana da Teoria da Resposta ao Item costuma-se representar a habilidade e conhecimento por uma variável aleatória simbolizada pela letra grega θ; a variável aleatória que representa o acerto ou erro de um item ´s simbolizada pela letra X; o resultado (acerto ou erro) de um item respondido é representado por X = x, onde X = 1 normalmente representa o acerto do item e X = 0 representa o erro. O gráfico da Curva Característica do Item acima é portanto um gráfico que associa a probabilidade de acerto P(X = 1 | θ) em função de θ. Adicionalmente costuma-se utilizar o índice i para indicar um examinando específico (θi representa a habilidade e conhecimento do examinando i) e o índice j para indicar um item específico (Xj representa os possíveis resultados do item j e Xij = xij representa a resposta do examinando i ao item j).
Existe uma gama extensa de modelos da Teoria da Resposta ao Item: os modelos mais complexos podem considerar uma multidimencionalidade da habilidade e conhecimento onde a variável teta que a representa é um vetor multidimencional θ = (θ1,θ2,...,θk) como também considerar a abordagem de créditos parciais para acomodar itens com estágios hierárquicos de desenvolvimento, por exemplo: primeiro estágio se nada está correto na resolução do item (Xj = 0j). segundo estágio se o item foi corretamente esquematizou o problema corretamente (Xj = 1j); terceiro estágio se o desenvolvimento do raciocínio está correto (Xj = 2j) e; quarto estágio se o item foi respondido corretamente na íntegra (Xj = 3j). O modelo de créditos parciais, embora pouco utilizado, é adequado para questões discursivas.
O modelo mais simples e usual da Teoria da Resposta ao Item considera itens dicotômicos (onde os possíveis resultados são acerto ou erro) e uma função logística para modelar a Curva Característica do Item:
Na modelagem bayesiana da Teoria da Resposta ao Item, conforme citado no início, diz-se que as respostas Xi = (xi1,xi2,xi3,...xiJ) onde J é o número de itens respondidos pelo examinando i estão correlacionadas através da habilidade e conhecimento θi do examinando. Se θi fosse conhecido, as respostas xi1,xi2,xi3,...xiJ seriam independentes estatisticamente. Essa abordagem costuma suscitar algumas confusões pois para o cálculo da verossimilhança utilizaremos o fato de que Xi1 | θ, Xi2 | θ, ..., XiJ | θ são independentes estatisticamente, ao passo que Xi1, Xi2, ..., XiJ são estatisticamente dependentes. Essa propriedade é conhecida comoindependência condicional e pode ser estudada em mais detalhes em artigo de De Finetti, B; por ora consideremos que se soubéssemos o verdadeiro valor da habilidade e conhecimento de um examinando as suas respostas a um conjunto de itens seriam estatisticamente independentes pois já saberíamos sua habilidade. Dessa forma, submetê-lo a um conjunto de itens seria inútil: os acertos e erros aos itens seriam meramente aleatórios. Para que a Teoria da Resposta ao Item seja aplicável é necessário pressupor que a habilidade e conhecimento de um examimando seja conhecido através de uma incerteza, representada por uma distribuição de probabilidade, e que os acertos e erros de um examinando numa prova revelem informações sobre seus conhecimentos e habilidades.
Considerando a propriedade da independência condicional dos acertos e erros dos itens respondidos por um examinando, a verossimilhança gerada pelas respostas de um examinando é dada por:
Após o examinando responder um conjunto de itens a estimativa da habilidade e conhecimento pode ser facilmente calculada através do Operador de Bayes:
Onde P(θi) é a distribuição de probabilidade a priori para a habilidade e conhecimento do examinando i, :L(θ | Xi = xi) é a verossimilhança gerada pelas respostas aos itens e P(θi | Xi = xi) é a distribuição de probabilidade a posteriori para o mesmo examinando ao responder os itens Xi = (xi1,xi2,...,xiJ).
Bibliografia
- Andrade, D. F., Tavares, H. R., Valle, R. C.(2000). Teoria da Resposta ao Item. Conceitos e Aplicações. Associação Brasileira de Estatística: São Paulo.
- Andrade, D., Valle, R. (1998). Introdução à Teoria da Resposta ao Item. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 18, 13-32.
- Angoff, W. (1971). Scales, Norms, and Equivalent Scores. In R. L. Thorndike (Ed.), Educational Measurement (2nd. ed.), Washington, D.C.: American Council on Education.
- Gulliksen, H (1950). Theory of Mental Tests. New York: Wiley.
- De Finetti, B. (1931). Funzione caratteristica di un fenomeno aleatorio. Atti della R. Accademia Nazionale dei Lincei, Serie 6. Memorie, Classe di Scienze Fisiche, Mathematice e Naturale, 4:251–299.
- Fletcher, P (1995). Procedimentos para Estabelecer a Equivalência de Provas com Modelos da Resposta ao Item. Ensaio. Rio de Janeiro. v. 3, n. 6, p. 41-54.
- Lord, F M.. (1977). Pratical Applications of Item Response Theory to Pratical Testing Problems. Hillsdale, New Jersey: Lawrence Erlbaum.
- Lord, F M., & Novick, M R, (1968). Statistical Theories of Mental Test Scores. Reading Mass: Addison-Wesley.
- Klein, R. (2003). Utilização da Resposta ao Item no Sistema Nacional de Avaliação da Educação Básica (SAEB). Ensaio: Avaliação e Políticas Públicas em Educação. Rio de Janeiro, 11, 40, 283-96.
- Mislevy, J., Bock, D (1990). BILOG 3: Item Analysis and Test Scoring with Binary Logistic Models. Chicago: Scientific Software Inc.
- Tavares, H. R. (2001). Teoria da Resposta ao Item para Dados Longitudinais. Tese de Doutorado. Universidade de São Paulo.
- Valle, R. (2000). Teoria da Resposta ao Item. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 21, 7-91.
- Valle, R. (2001). Construção e Interpretação de Escalas de Conhecimento: um Estudo de Caso. Estudos em Avaliação Educacional. São Paulo: Fundação Carlos Chagas, 23, 71-92.



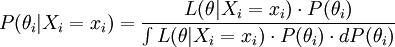
Nenhum comentário:
Postar um comentário